Introdução ao Perceptron multicamadas passo a passo

Olá meus queridos sete leitores!

Para você que vem estudando Machine Learning ou se deparou com esse tópico na faculdade já deve ter encontrado em seu caminho um modelo chamado perceptron multicamadas do inglês Multilayer perceptron.

Para aqueles que querem se  aprofundar nos estudos de redes neurais artificiais e nas aplicações desses modelos matemáticos fascinantes é de extrema importância entender a topologia dessa rede e um pouco algoritmo utilizado para a otimização.

No post de hoje iremos fazer um tutorial simples desse modelo e do algoritmo gradiente descendente que pode ser usado para treiná-lo.  Aqui irei focar na simplicidade e mostrar a forma mais básica desse modelo. É importante lembrar que existe uma enorme quantidade cálculos envolvidas no processo, porem são cálculos simples que podem ser aprendido se forem estudados com calma de forma separada. Convido a você dar uma olhada nesse post como um ponta pé inicial para se aprofundar em deep learning. A ideia de MLP vai nos da uma generalização, mesmo que simples nesse caso, do principal problema que estamos interessados em solucionar

Antes de entrar de cabeça no post é interessante que você saiba como funciona o modelo Perceptron. Eu fiz um post sobre o assunto:  Introdução ao perceptron passo a passo.

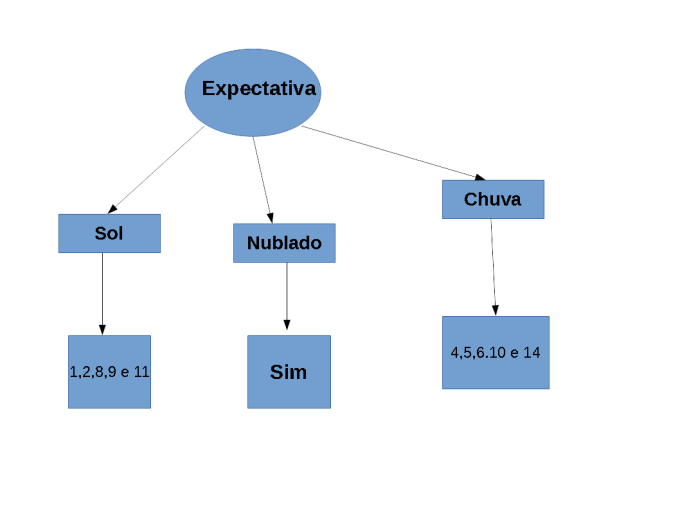
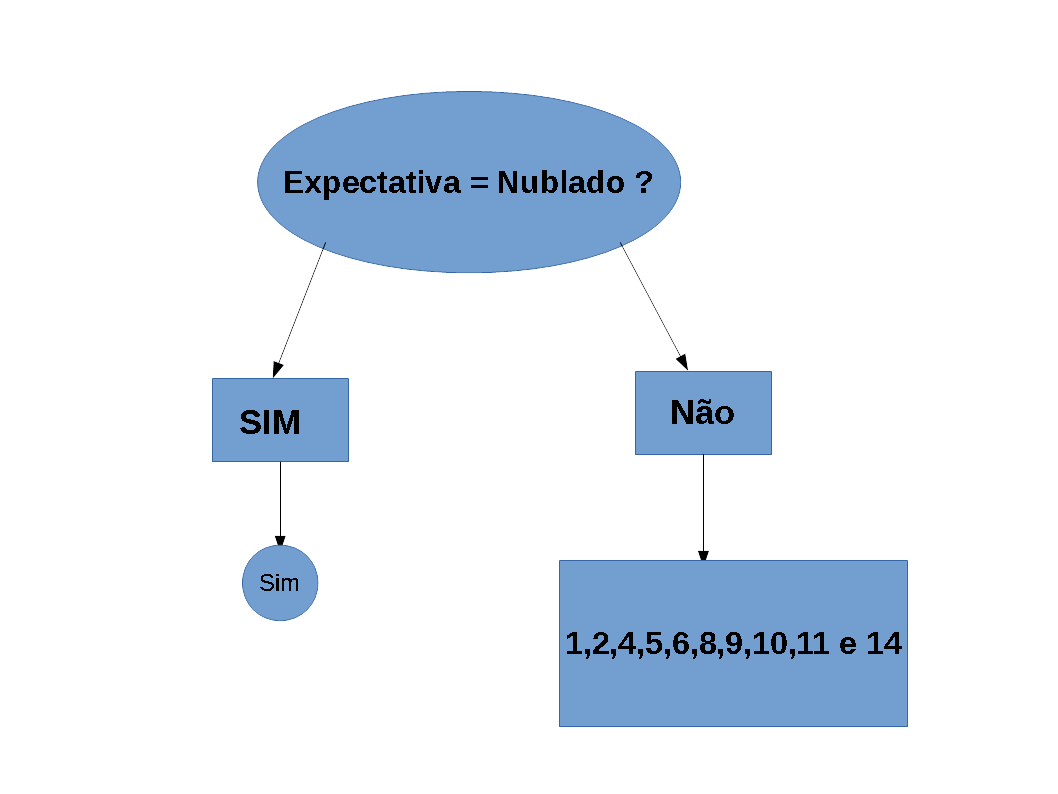
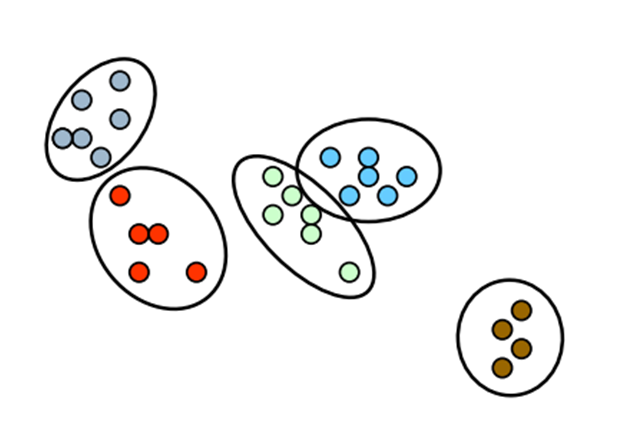
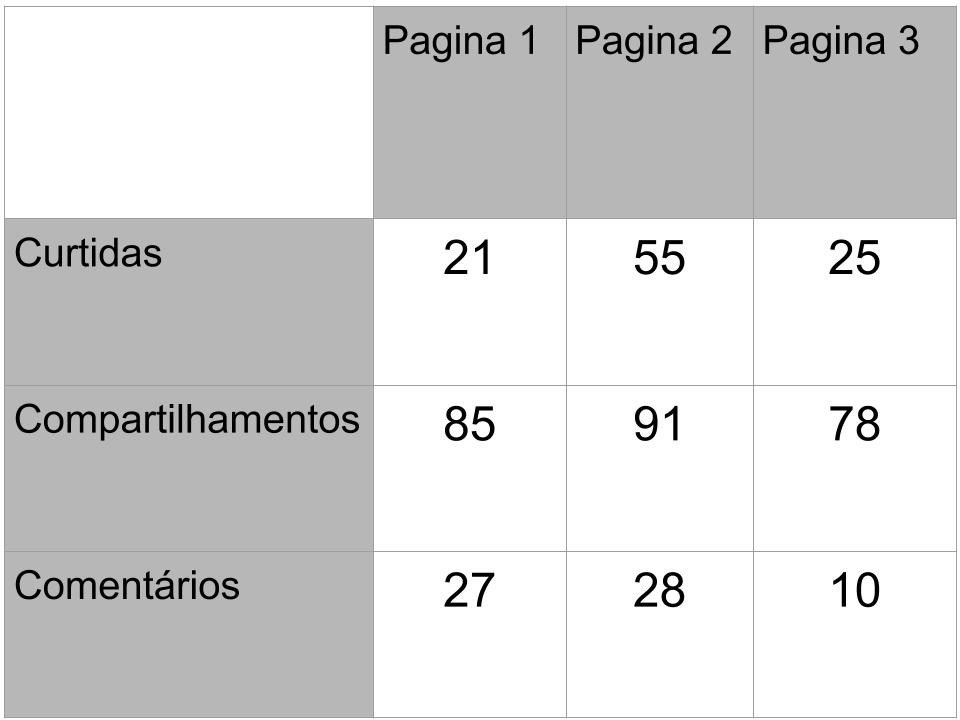
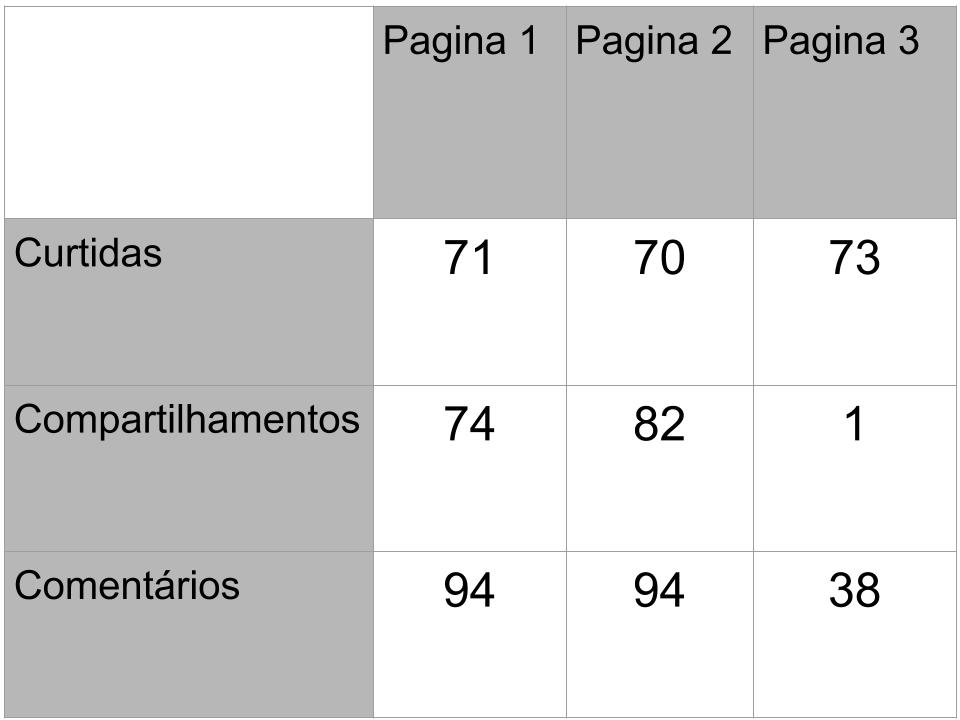
Para você que já entendeu como funciona o perceptron deve ter notado também sua limitação quando aplicado a problemas de classificação. Ele apenas resolve problemas em que os dados são linearmente separáveis. Ou seja, situações em que é possível traçar uma “reta” entre os dois conjuntos.

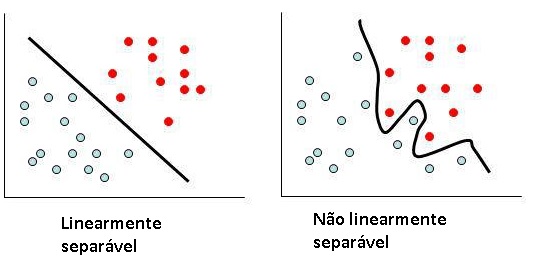
Hoje iremos focar no  tipo de problema representado à direita.

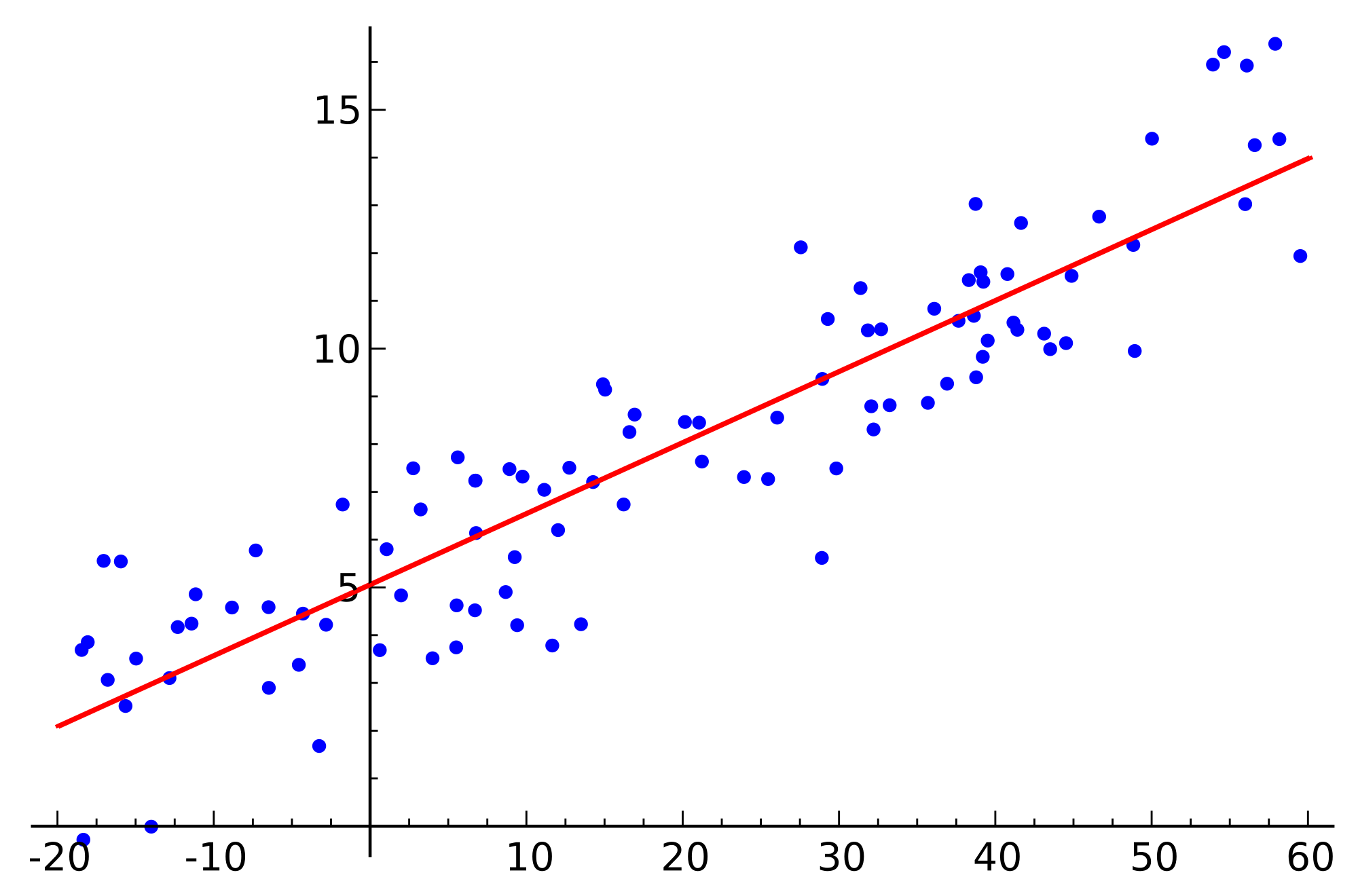
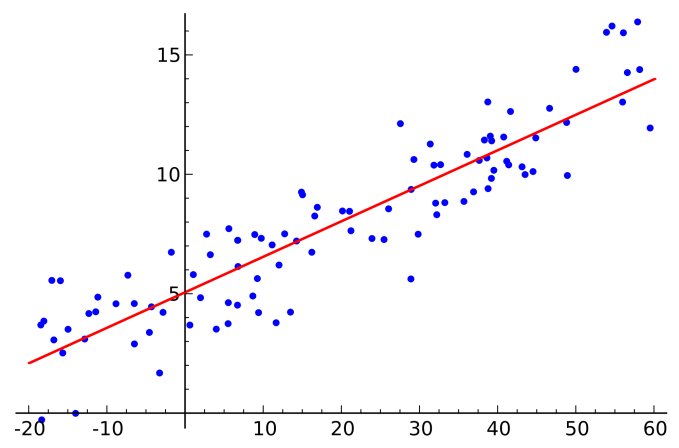
Para isso vamos usar um conjunto de dados fictício representado no gráfico abaixo:

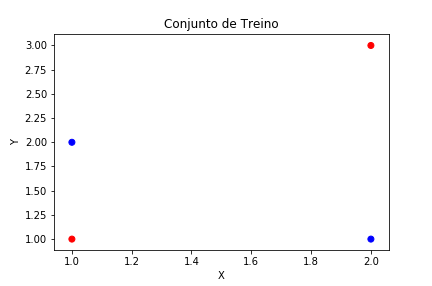
Repare que nessa situação é impossível traçar uma reta que divide os conjuntos em duas partes. Logo, não é possível resolver o problema utilizando um simples Perceptron.

Observação!! : A escala dos dados aqui estão entre 1 e 3. Ná prática é necessário reescalar seus dados pois o MLP é sensível a escala dos dados e isso pode gerar uma série de inconsistência numéricas, irei discorrer sobre isso em post futuros, mas para esse exemplo irei deixar dessa forma para facilitar um pouco mais os cálculos.

O modelo Perceptron multicamadas

Multilayer Perceptron, apesar do nome, não se refere a um perceptron com múltiplas camadas. Tecnicamente ele seria composto de vários perceptrons, mas só tecnicamente, pois pela definição o Perceptron é um tipo especial de rede neural que apenas realiza classificação binária. 

No nosso caso é importante saber que graças a essa camada oculta (hidden layer) podemos captar novos padrões . É possível aprender funções polinomiais e não lineares em geral.

Segundo o teorema de George Cybenko um multilayer perceptron com uma função de ativação sigmoide é um aproximador universal para qualquer função de base real. Mas não irei entrar em detalhes sobre isso. O que nos interessa por hora é aprender o básico de como esse modelo é otmizado.

Definindo o modelo e os parâmetros

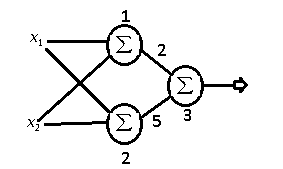
Para resolver esse problemas utilizaremos a seguinte a arquitetura:

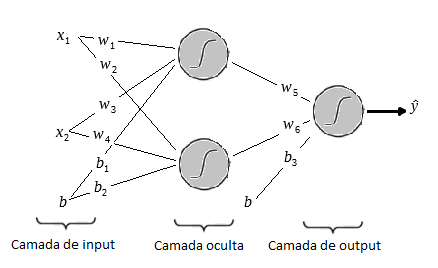
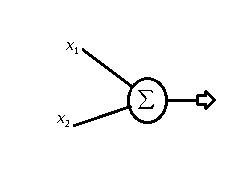
Na figura acima temos o layer de input com os dois inputs e mais o bias .

Uma observação sobre o bias é que ele sempre levara o input 1, o que importa de fato são os pesos e . Logo depois temos os pesos da primeira camada que vai de ate .

Uma vez que multiplicamos os pesos e adicionamos os biases aplicamos a função sigmóide e o mesmo processo é feito nos outputs da primeira camada até gerar os outputs da rede.

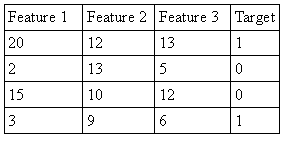
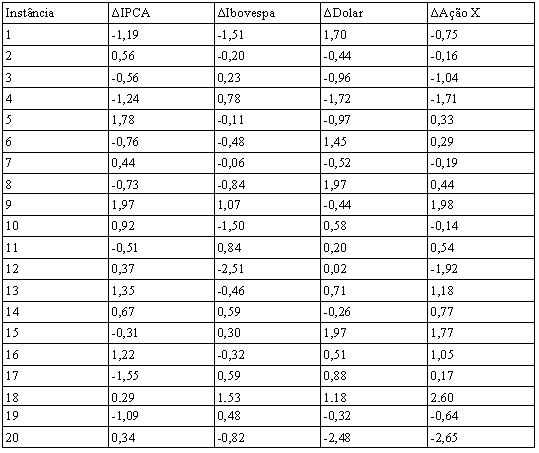
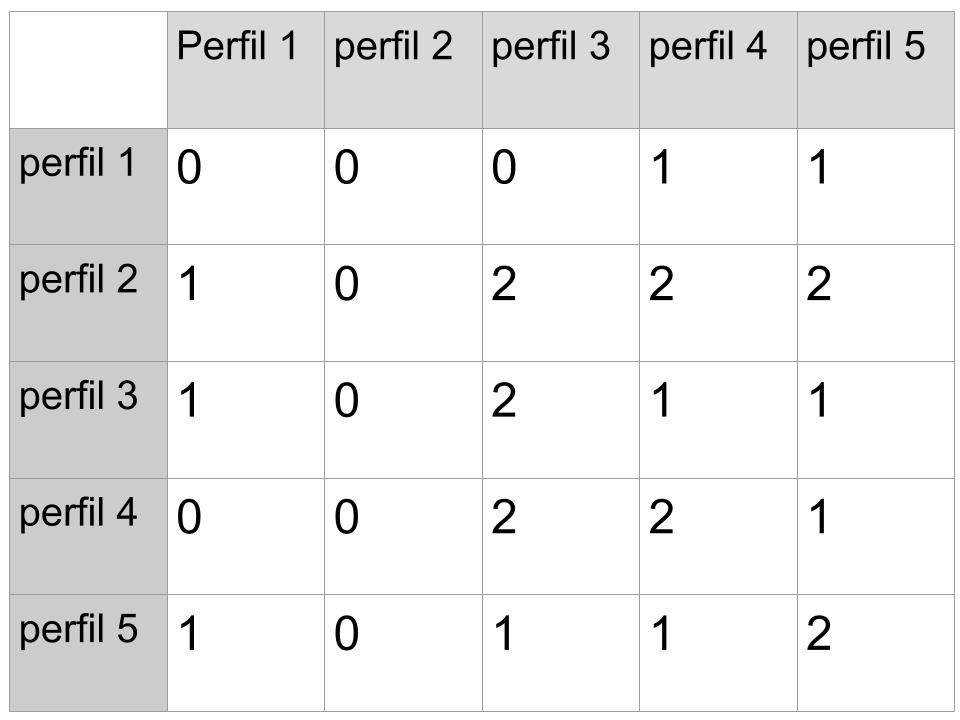
Organizamos o conjunto de treino em uma tabela que pode ser visualizada abaixo:

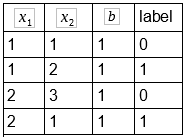
Repare que na coluna temos apenas o número 1. Isso é um truque metodológico para deixar a ideia de bias mais intuitiva.

Vamos agora definir nossos pesos iniciais de forma aleatória.

Definimos os biases:

Agora definimos os parâmetros da rede e a função de ativação:

Aqui definimos o alpha, a taxa de aprendizado, esse parâmetro regula a velocidade com que a rede irá aprender. Usei um alpha menor pois vi que com valores maiores a rede pode simplesmente passar do ponto ótimo.

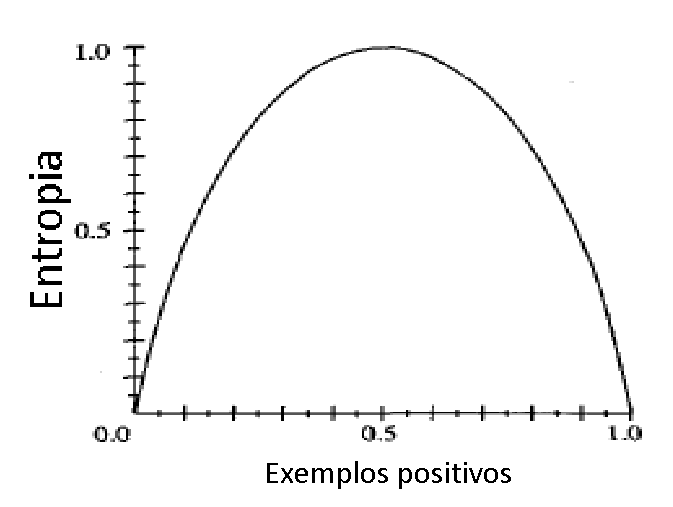
A seguir à função de ativação sigmóide que irá gerar o output de cada neurônio. A função sigmóide é interessante pois tende a 1 quando x tende ao infinito e tende a 0 quando x tende ao infinito negativo. Ela nos dá um discriminante em 0.5  acima disso posso classificar como positivo e abaixo como negativo por exemplo.

O aqui se refere ao resultado da multiplicação dos inputs pelos pesos de cada neurônio, antes de aplicar uma ativação dado um neurônio  qualquer o seu valor será dado por:

Aqueles da área de estatística podem estranhar a fórmula acima pois falta acrescentado ao resultado. Porém para esse tutorial irei tratar o bias como um input, lembre-se da coluna contendo apenas o número 1.

Dessa forma multiplicamos todos os inputs e adicionamos ao somatório.

Nossa função de perda(Loss Function.) será o erro quadrático médio.

Aqui o erro é dado pela média da soma dos quadrados das diferenças dos outputs da rede em relação a label original . O número  2 no denominador vai nos ajudar na hora de calcular a derivada do erro.

Temos que minimizar esse erro e assim achar o melhor conjunto de parâmetros e que nos dará o modelo ótimo para esse tipo de problema.

Antes de partir para o treino vamos tentar entender como é gerado o output final do MLP.

Entendendo como a informação é processada

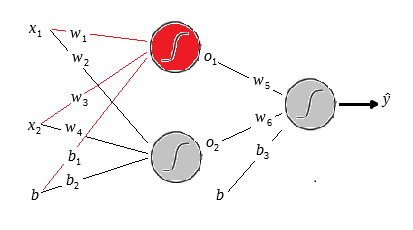
Na figura abaixo iremos calcular o output do neurônio vermelho. Aqui e são os outputs dos dois neurônios das camadas ocultas respectivamente, depois de aplicar a função sigmoide.

Na figura temos o vetor de input que será é representado por:

E repare que temos o vetor de peso, as arestas em vermelho que é representado por:

Multiplicaremos cada input pelo seu respectivo peso e somaremos o resultado. Isso nada mais é do que o produto entre dois vetores.

Vamos substituir o vetor de input pela terceira linha do conjunto de treino(Pois a primeira tem apenas 1 e pode ficar confuso) e o vetor de pesos pelos seus respectivos pesos e realizar a multiplicação.

Esse é o resultado da multiplicação do input pelos pesos correspondente da camada, após isso vamos aplicar a função sigmoide e dessa forma gerar o output do neurônio em vermelho.

No estado atual esse seria o output do neurônio vermelho.

Fazemos o mesmo procedimento para obter o output do outro neurônio.

depois basta aplicar a sigmoid:

Dessa forma obtemos o output da primeira camada. Veja no desenho abaixo.

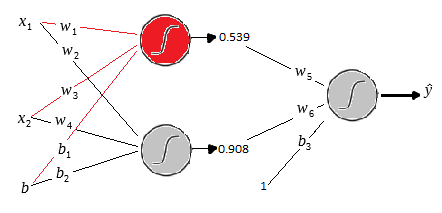
Olhe com atenção a mecânica dos cálculos, pois assim ficará mais fácil entender como é feito o treino da rede.

Vamos calcular o output final da rede. Repare que temos os pesos e   mais o bias que leva como input o número 1.

Agora basta substituir os valores:

Aplicamos a função sigmóide para gerar o output final da rede:

Esse é o output da rede para a terceira linha do nosso conjunto de treino. Se está certo ou errado depende da forma que decidir o discriminate.

É comum usarmos uma regra do tipo:  Acima de 0.5 é igual a 1 e abaixo de 0.5 é igual a 0. Por essa regra a predição estaria errada e teríamos que otimizar a rede.

Treinando o Perceptron Multicamadas

A primeira coisa a fazer agora é calcular os outputs para todos os exemplos do conjunto de treino abaixo.

Como foi demonstrado acima a forma que o MLP processa a informação irei me abster de realizar os cálculos e já podemos demonstrar o resultado de cada output na coluna net_out.

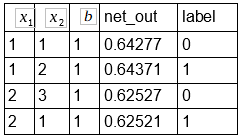
Com isso feito podemos medir o erro quadrado médio:

Logo basta somar os quadrados das diferenças dos outputs da rede em relação às labels e dividir pela quantidade de exemplos vezes 2. Lembrando que multiplicamos por 2 apenas para facilitar o cálculo da derivada.

Dê uma olhada no cálculo abaixo:

Aqui tivemos um erro quadrado médio de 0.13393.

Agora que sabemos o erro podemos iniciar a propagação do erro para as camadas e atualizar cada peso conforme a regra abaixo.

Onde será o valor do peso após a atualização,  o valor atual do peso, a taxa de aprendizado que definimos,aqui é 0.01, e é o gradiente do erro em relação ao peso que iremos atualizar.

Mas antes voltemos ao esquema da rede.

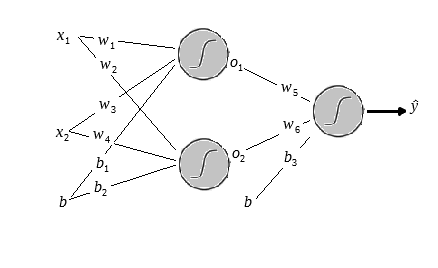
Repare que para atualizar um peso dessa rede teremos que achar o gradiente do erro em relação ao peso que iremos utualizar.

Iremos realizar a primeira atualização da rede passo a passo de forma bem simples.

A primeira coisa que temos que fazer é achar a derivada do erro total em relação ao output . Basta definir a derivada da função de perda.

Logo:

A conclusão que chegamos aqui é que a derivada de em relação a  é nada mais do que erro médio.

Antes de ir para o próximo passo observe o desenho a abaixo:

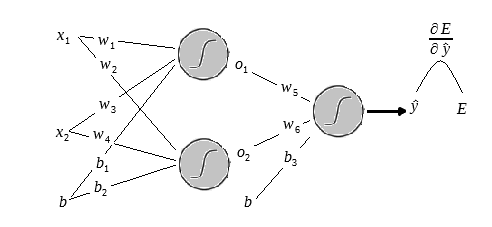
Acrescentei no final a letra para dar uma ideia de como o erro se relaciona com o output da rede e para mostrar de forma esquematizada a derivada do erro em relação ao output.

Agora iremos achar a derivada do output da rede em relação a . Lembre-se que após a multiplicação pelos pesos é aplicado a função sigmóide ao resultado:

Não irei entrar no mérito de derivar a função sigmóide aqui. Dado que o post já está grande demais. Porém você pode dar uma olhada neste excelente post do portal Towards Data Science que mostra de maneira detalhada o processo de derivação dessa função:

https://towardsdatascience.com/derivative-of-the-sigmoid-function-536880cf918e

Assumimos que a derivada do ouput em relação ao resultado da camada anterior é dada pela parcial:

Onde é a função sigmóide aplicada ao resultado da multiplicação da camada anterior pelos pesos subsequentes. Repare que é uma derivada parcial pois irei deixar as outras variáveis constantes.

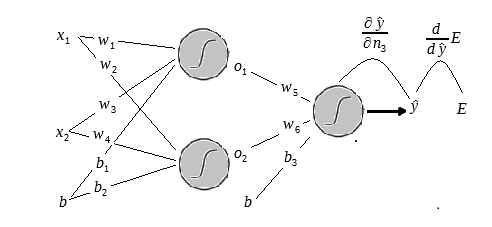
Repare que é o output da rede. No caso é a função sigmóide aplicada ao resultado da multiplicação dos outputs da camada subsequente que são e  pelos pesos e e adicionado do bias. Entenda bem isso pois quando formos propagar o erro para camada de input iremos derivar em relação a esses dois outputs também.

O próximo passo é a parcial do output em relação ao um dos pesos.

vamos atualizar agora:

Observe a figura abaixo:

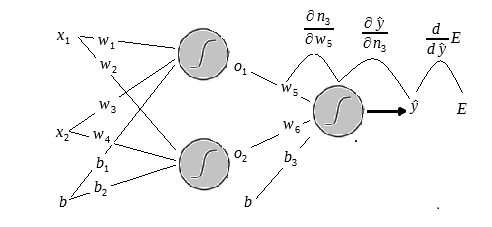
Aqui concluímos que a derivada parcial do resultado em relação ao peso   é o próprio input que multiplica esse peso.

Porém o que interessa aqui é saber a derivada parcial do erro em relação a esse peso. Para isso basta utilizar a regra da cadeia.

Ou seja:

Uma observação importante: Irei utilizar a média dos valores dos gradientes dos outputs para atualizar o peso. Na fórmula acima temos a regra para atualizar com base em um único output, estocástica, porém iremos atualizar de forma direta, utilizando todo o conjunto de treino.

Vamos começar vendo a derivada do erro atual em relação ao output da rede :

O próximo passo é calcular o o gradiente do output em relação a .

É importante lembrar aqui que como estamos trabalhando com um batch o que teremos na verdade é a média dos gradientes de cada erro em relação ao peso em questão.

Vamos dar uma olhada nisso mais de perto. Como vimos a derivada da sigmoid é dada por:

O gradiente para o primeiro input seria:

Mas o que queremos é a média de todas as derivadas de um dado Batch. No nosso caso todo o conjunto de treino.

Logo teremos:

Agora basta achar a derivada do resultado em relação ao peso :

Como queremos a média de todos outputs do batch basta somar todas as saídas de :

Logo teremos:

Agora pela regra da cadeia temos que:

Com isso temos o gradiente do erro em relação ao peso . Como temos um erro positivo é correto pensar que temos que diminuir o valor do peso para que tenhamos um erro menor.

Vamos antes lembrar alguns parâmetros da rede.

O primeiro é a taxa de aprendizado que foi definida em 0.01. O segundo é o peso antigo que foi inicializado como 1.32.

logo temos:

E agora basta aplicar a regra de atualização:

Com isso concluímos a atualização do primeiro peso da rede.

Temos agora:

Vamos fazer o mesmo procedimento para, abaixo temos o valor inicial do peso:

Lembrando que a derivada parcial de em relação a é dada por:

Dae basta pegar a média dos gradientes de de em relação a :

Aplicamos a regra da cadeia:

Se aplicarmos o mesmo procedimento ao bias   teremos:

Aqui é importante lembrar que o input do bias é sempre 1. por esse motivo a derivada do bias é igual a 1. depois basta tirar a média de todas as derivadas dos inputs que compõem o conjunto de treino.

É interessante notar que a derivada do bias é 1 justamente por esse ser o coeficiente linear da equação que compõe o output.

E finalmente calculamos a derivada do erro em relação ao bias:

Com isso em mãos podemos atualizar o bias dessa camada:

Até aqui já atualizamos a última camada da rede.

Porém agora atualizaremos os pesos da primeira camada. partiremos do peso .

Antes precisamos entender como o erro varia em relação a esse peso.

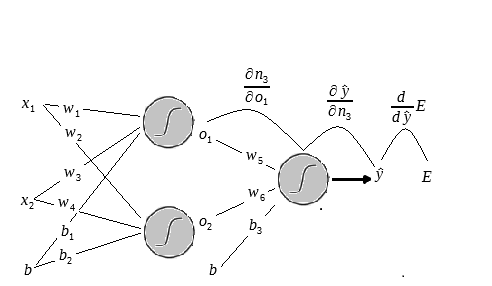
Se olhar na figura anterior podera ver que derivamos o erro ate em relação a porem agora encaixaremos mais uma peça na nossa figura.

Para calcular a variação do erro em relação a é necessário obter as seguintes derivadas.

Repare que não derivamos o erro mais em relação a pois nessa etapa ele é considerado como uma constante e o que será considerado como uma variável.

Vamos começar o processo. Como vimos antes já possuímos os gradientes do erro até em relação a calculados.

Logo vamos adicioná las a fórmula:

Lembrando que os valores se referem a média das derivadas do batch todo. Vamos calcular a próxima parte dessa derivada:

Como vimos:

Logo:

A diferença dessa derivada em relação a que derivamos na outra vez é que aqui derivamos em relação a e não em relação a .

Como sabemos que inicial é igual a 1.32 basta multiplicar por 4 e dividir por 4. É bem óbvio que o valor será o mesmo, porém é interessante ilustrar.

Agora vamos à próxima derivada.

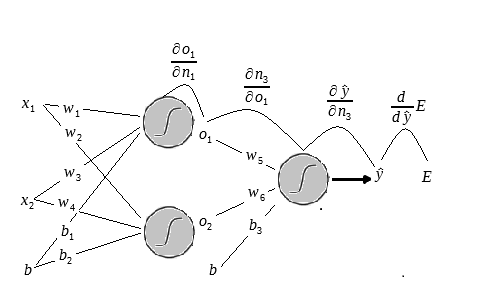
Sabemos que:

Logo:

Agora pegamos a média dos gradientes para o batch:

Agora basta encaixar esse resultado na equação:

O próximo passo é achar o gradiente de em relação a :

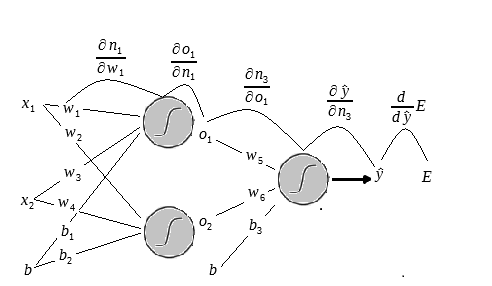
logo:

Calculamos a média de todos os inputs para :

Encaixamos isso na equação para obter o resultado final, a variação do erro em relação ao peso .

Com isso em mãos pode-se aplicar a regra de atualização. (Delta rule.) e atualizar o peso

Irei aplicar o mesmo procedimento ao peso e o bias . Por hora irei pular os cálculos. Mas a ideia é a mesma, a única coisa que muda é que será calculado a deriva em relação a aquele peso ou bias.

Como já temos a derivada parcial até o neurônio basta apenas calcular a derivada em relação a que como já vimos é o próprio input  .

Temos que:

Fazemos a atualização:

Vamos atualizar o bias agora:

Com isso feito. Atualizamos os pesos que geram o output de primeiro neurônio da primeira camada oculta .

Ainda falta fazer a atualização dos pesos , e o bias que geram o output . Nesse momento iremos ter que achar a derivada de em relação a .

Veja a figura abaixo:

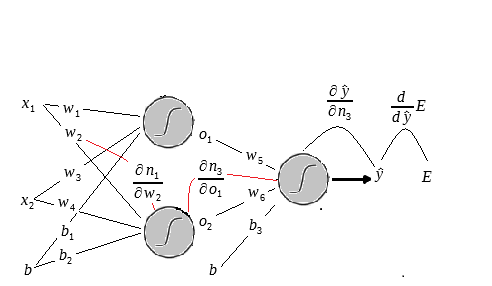
As linhas pretas indicam as derivadas que já possuímos e as vermelhas indicam as que devemos calcular agora.

Vamos iniciar calculando a derivada em relação a :

Voltando a equação da cadeia com os gradientes que já possuímos vemos que:

Vamos calcular a próxima derivada:

Calculamos a média de para todos os elementos do batch que no caso é igual ao próprio .

E encaixamos isso na nossa equação:

Agora é hora de achar a próxima derivada da equação.

sabemos que:

logo:

Agora basta pegar a média dos gradientes para o neurônio :

Encaixamos mais esse resultado em nosso equação:

Agora iremos derivar a última parte. E como já vimos:

Agora basta adicionar a média dos quatro inputs em nossa equação:

Com isso em mão podemos atualizar o peso :

Como já sabemos que o processo é o mesmo para o peso e o bias irei já colocar o valor atualizado de cada um:

E com isso temos todos os pesos e biases atualizados e a primeira iteração terminada:

Agora vamos recalcular os outputs da rede e comparar os erros quadráticos médios:

Primeiro pegamos a tabela contendo todos os novos outputs da rede:

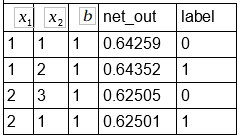
O erro depois da atualização ficou em: 0.13390 houve pequena redução em relação a 1.3393.

Com isso encerramos a primeira época. Caso continuemos com o treino iremos repetir esse processo até minimizar o erro ao valor mínimo.

Repare que houve uma diminuição em todos os valores da rede. Isso ocorreu pois por hora todos os valores de outputs ainda estão acima de 0.5.

Para você que se interessou pelo post vale a pena tentar reproduzir o procedimento em uma linguagem de programação e analisar a convergência da rede.

Gostaria também de lembrar ao leitor que para fazer esse post foi necessário uma grande quantidade de cálculos manuais e então infelizmente existe uma probabilidade de erro e inconsistências e caso veja alguma coisa errada pode está entrando em contato com autor pois assim estará colaborando para o desenvolvimento de material de qualidade para a comunidade.

Até o próximo post e bons estudos.

Uma introdução ao TensorFlow e suas operações básicas

Ola pessoas. Se você veio ate aqui já deve ter uma ideia do que se trata o post de hoje. A um tempo que venho estudando TensorFlow e aprendendo aos poucos a sua lógica.

Primeiramente tentaremos definir o porque do nome TensorFlow. Eu acho que é provavelmente devido ao uso intenso das estruturas chamada Tensores.

Meio óbvio. Mas o que será realmente um Tensor? Bem definir um tensor de maneira formal não é uma tarefa fácil.

Mas vamos a algumas definições e exemplos básicos você verá que entender de maneira intuitiva não é uma missão tão difícil.

Mas vamos aproveitar e definir algumas estruturas mais básicas.

Vetores

Para quem já tem intimidade com Álgebra linear já é acostumado com essa estrutura.

Podemos por exemplo representar a linha ou coluna de uma tabela por meio de um vetor.

A primeira linha da tabela pode ser representada por um vetor:

ou

Podemos representar essa estrutura de dados em Python e você já deve saber como:

A = [20,12,13,1]

Vamos parar por aqui e analisar mais uma estrutura interessante.

Matrizes

Umas das estruturas mais utilizadas em Machine Learning e principalmente Deep Learning é a tão famosa matriz.

Podemos representar toda a tabela acima por meio de uma matriz:

Agora podemos nos referir a cada elemento dessa matriz por meio de um índice duplo. Por exemplo o elemento  é 5.Ou seja o terceiro elemento da segunda linha.

Também podemos representar essa estrutura em Python:

A = [[20,12,13,1],
 [20,13,5,0],
 [15,10,12,0],
 [3,9,6,1]
 ]

E claro podemos ter acesso aos seus elementos quase da mesma forma.

In [1]: A[1][2]
Out[4]: 5

Difere apenas no fato de que na maioria de linguagem de programação os indices começam em 0 enquanto na matemática começa e 1.

Isso dito vamos a uma estrutura não tão popular assim.

Tensor

Suponha que você queira representar uma imagem por meio de uma lista ou array. Suponha a imagem abaixo.

Apenas a título de exemplo suponha que tenhamos a ideia de representar essa imagem usando um padrão RGB e para facilitar ainda mais as coisas suponha que seja uma imagem 4 por 4.

Acima temos uma Matriz de rank 3. Em outras palavras um tensor, claro que a definição do ponto de vista matemático seria bem mais sofisticada que isso, mas por hoje podemos nos limitar a definir um tensor como uma matriz de 3 ou mais dimensões.

Uma outra forma de representar a imagem acima seria:

Se pararmos para pensar. No ponto de vista da programação as estruturas de dados vistas aqui são bem semelhantes e podemos representá-las de várias maneiras diferentes.

Podemos, por exemplo, representar uma lista de duas dimensões(Matriz) por meio de um vetor.

In [1]: import numpy as np
In [2]: matrix = np.array([[1,2,3],[4,5,6]])
In [3]: vector = matrix.ravel()
vector
Out[4]: array([1, 2, 3, 4, 5, 6])

Entender essa estrutura é essencial para tirar o máximo proveito das redes neurais artificiais e sistemas de aprendizado mais complexos.

Operações básicas em TensorFlow

É importante lembrar que o TensorFlow não compila e executa o programa ao mesmo tempo, ele primeiro compila e depois executa o programa, para isso temos a classe Session. Veja o exemplo abaixo onde multiplico dois números.

 

import tensorflow as tf

#Primeiro definimos os números

#criamos uma constante.
x_1 = tf.constant(2.0,dtype=tf.float32)

#A função tf.constant cria nossas constantes
x_2 = tf.constant(5.0,dtype=tf.float32)

#Aqui multiplicamos os dois resultados.
mult = x_1*x_2

#Aqui somamos as duas constante
soma = x_1+x_2

# Toda vez que quisermos executar usamos o método run
# Isso nos permite compilar e executar o código solicitado.
sess = tf.Session()

#Aqui executamos a multiplicação
print(sess.run(mult))

#Aqui executamos a soma.
print(sess.run(soma))

Quando rodar isso terá o seguinte resultado:

10.0
7.0

Na primeira linha o resultado da multiplicação e na segunda o resultado da soma.

O processo de soma e multiplicação de vetores não é muito diferente, porem é preciso lembrar das propriedades das operações com vetores.

criamos uma variável constante.
vetor_1 = tf.constant([2.0,3.0,7.0],dtype=tf.float32)

#A função tf.constant cria nossas constantes
vetor_2 = tf.constant([5.0,2.0,6.0],dtype=tf.float32)

#Aqui multiplicamos os dois vetores
#Utilizei as funções multply e reduce_sum.
#multply: multplica duas array elemento por elemento.
#reduce_sum: faz o somatório dos elementos de um vetor
mult = tf.reduce_sum(tf.multiply(vetor_1,vetor_2))

#Aqui somamos os dois vetores de forma tradicional
soma = vetor_1+vetor_2

# Toda vez que quisermos execultar o métono run
# Isso nos permite compilar e execultar o codigo solicitado.
sess = tf.Session()

#Aqui execultamos a multiplicação
print(sess.run(mult))

#Aqui execultamos a soma.
print(sess.run(soma))

Pronto fizemos as operações básicas com vetores basta rodar e ver o resultado.

58
[7. 5. 13.]

Vamos analisar uma outra função a tf.add essa função nos permite ligar de forma intuitiva vários Nodes de um grafo. Vejamos um exemplo simples.

Vamos processar a seguinte estrutura representada no esquema abaixo.

Nesse exemplo duas variáveis e  entram como input e são somadas e logo depois gerado o output.

#tf.placeholder funciona como um input.
#isso quer dizer que essas variáveis virão de fora
x_1 = tf.placeholder(dtype=tf.float32)

#Aqui os valores entrarão somente ná hora que
# forem execultados.
x_2 = tf.placeholder(dtype=tf.float32)

output = tf.add(x_1,x_2)

# Toda vez que quisermos execultar o métono run
# Isso nos permite compilar e execultar o codigo solicitado.
sess = tf.Session()

#Aqui execultamos a soma.
#Repare que passamos os valores para os placeholders na forma
# de um dict. Eu acho isso interessante pois facilita a comunicação
# com a API.
print(sess.run(output,{x_1:1,x_2:2}))

Quando executar terá o seguinte output:

3.0

Vamos a uma estrutura um pouco mais intrigante.

Nesse caso temos uma estrutura semelhante ha de uma rede neural artificial, claro falta algumas coisas, mas como o foco é o processamento da informação isso não é um problema.

Numerei os Nodes de 1 a 3 os inputs entram e são somados em cada Node e depois o resultado de cada um é multiplicado por uma constante e o output sai no utimo Node.

#Vamos declarar os inputs
x_1 = tf.placeholder(dtype=tf.float32)

x_2 = tf.placeholder(dtype=tf.float32)

#Crio o primeiro Node
#Ele soma os dois inputs
Node_1 = tf.add(x_1,x_2)

#Crio o segundo Node
Node_2 = tf.add(x_1,x_2)

#No terceiro Node esses valores entram Multplicados
#Pelos seus respectivos pesos
Node_3 = tf.add(Node_1*2,Node_2*5)

# Toda vez que quisermos execultar o métono run
# Isso nos permite compilar e execultar o codigo solicitado.
sess = tf.Session()

#Aqui execultamos a soma.
#Repare que passamos os valores para os placeholders na forma
# de um dict.
print(sess.run(Node_3,{x_1:8,x_2:9}))

 

O output deve ser:

119.0

Lembro que isso é apenas uma introdução simplista ao TensorFlow. A ideia aqui e te mostrar uma ligação entre os FrameWork e a Álgebra Linear.

Na Prática é comum trabalha com a ideia de  vetores e matrizes para fazer as operações de treinamento de um algoritmo.

Aconselho que antes de usar o TensorFlow domine muito bem os conceitos teóricos relacionados ao algoritmo, pois isso irá lhe permitir usar ao máximo o poder que essa ferramenta tem a oferecer.

Muito bem por hoje é só. Ate a próxima e bons estudo.

E como sempre qualquer dica, critica e inconsistencia no post deixe nos comentários o intuito é sempre a melhora do conteudo.

Classificação e regressão com K-nearest neighbors

Como muitos já devem saber, o algoritmo K-Nearest Neighbors e os métodos derivados são extremamente básicos para qualquer um que planeje se aventurar no Machine learning. E, por esse motivo, muitas pessoas passam direto por ele achando que é uma técnica fraca.

Apesar das limitações relacionadas a escala vs tempo de processamento, o K-NN nos permite resolver alguns problemas de forma simples. E quando temos uma boa seleção de features e amostras, ele pode nos render insights valiosos e se tornar um classificador poderoso.

Pensando nisso, resolvi escrever esse post sobre as estratégias do K-NN para problemas de classificação e regressão, também relatar um pouco sobre os modelos usados em cada problema.

Nas questões de classificação analisaremos dois cenários: um onde temos poucas classes, e o outro onde temos muitas classes. E discorrer sobre as estratégias para resolver cada um dos problemas.

Nos problemas de regressões analisaremos duas estratégias que podem ser usadas com o K-NN para se conseguir bons resultados.

Caso você ainda não conheça esse algoritmo, escrevi alguns posts sobre ele:

K-nearest neighbors com scikit learn

K-nearest neighbors seu primeiro algoritmo de machine learning

Vantagens e desvantagens

Antes de partir para uma análise mais aprofundada do modelo, é preciso alertar para algumas características do mesmo.

O primeiro problema que surge é relacionado a dimensionalidade do inglês (curse of dimensionality), isso deve ser observado, pois na prática, o número de atributos/variáveis envolvidos em um problema tendem a aumentar.  Isso faz com que os vetores usados pelo K-NN para cálculo das distâncias tenham dimensões muito grandes, o que acaba atrapalhando a localização de alguns padrões relevantes.

Irei reservar um post para falar sobre o tema curse of dimensionality.

A boa notícia é que uma vez que conseguir reduzir o número de dimensões, ou achar os atributos mais relevantes, ele irá funcionar muito bem, e você terá em mãos um modelo fácil de interpretar; o que é útil para a geração de insights.

Outro problema relacionado ao K-NN, é em relação ao processamento necessário na hora de fazer uma predição, por ser um algoritmo que não gera um modelo, mas ao invés disso calcula a distância da instância em relação a todas as outras do conjunto de treino que foi usado para treiná-lo. Isso gera uma enorme necessidade de processamento o que pode até inviabilizar o seu uso em aplicações reais.

Felizmente existem métodos como KD-tree e Ball-tree para lidar com esse tipo de problema, falarei desses métodos futuramente. E há casos em que a quantidade de dados não é tão grande, por isso podemos facilmente usar métodos de programação avançada para acelerar o tempo de predição.

Classificação

Com certeza a aplicação mais comum do K-NN é em problemas de classificação.

Nesse caso, a forma mais utilizada para se medir a distância entre os pontos, é a boa e velha distância Euclidiana.

Ela calcula a distância entre dois vetores (que no caso acima foram representados como sendo linhas de uma matriz), que é sua representação mais comum em aplicações reais.

O K-NN procura então achar os K vizinhos mais próximos de um dado ponto no espaço, então o mesmo procura pelo seguinte conjunto de vetores:

Onde são linhas da matriz , enquanto que e são os números de vizinhos, e número de elemento do vetor respectivamente, e é a instância que será classificada.

Isso retornará um conjunto de vetores no qual a soma das distâncias entre eles e a instância que será classificada, seja a menor possível.

Por exemplo, caso definirmos K igual a 3 teremos três vetores nesse conjunto.

Feito isso, é preciso saber qual a classe dominante nesses vetores. Cada vetor do conjunto está associado a uma classe. Para descobrir a qual classe a instância pertence, é feita uma votação para saber em qual classe ela se encaixa. Definimos a instância em questão como pertencendo a classe que tenha maior ocorrência no conjunto que retornar da iteração.

Podemos definir isso de maneira formal usando o conceito de proporção.

No vetor podemos extrair classes de elementos contidas no vetor, a partir daí basta aplicarmos o seguinte passo.

Onde é uma função de perda do tipo:

Podemos ler a expressão acima como:

“A probabilidade de pertencer a classe é igual a soma das ocorrências positivas dividida pela quantidade de vizinhos mais próximas da instância.“

Classificamos a instância como sendo da classe com maior proporção de ocorrência.

Para problemas de classificação com poucas classes, esse método pode ser interessante, porém, em problemas com muitas classes pode acontecer de classificarmos uma instância erroneamente por falta de exemplos da classe que ela pertence. Em caso de pequenos, ou o contrário, pode haver muitos vizinhos que estão distantes da instância terém um peso muito grande e atrapalhar a classificação da instância em casos onde é muito grande.

Para resolver essa questão, podemos usar a distância ponderada. Uma maneira muito popular de lidar com esse problema é usar o inverso da distância euclidiana:

Onde é um vetor do conjunto dos vizinhos mais próximos, o número de elementos/dimensões do vetor e a instância que será classificada.

Agora, ao invés de avaliarmos as classes dos vetores mais próximos, passamos a avaliar seus pesos. Daí avaliamos a instância como pertencendo a classe na qual a soma dos inversos das distâncias em relação a ela seja a maior possível.

Com isso em mãos, podemos lidar melhor com os problemas que envolvem muitas classes, pois damos menos importância aquelas que estão mais distantes da instância a ser classificada. Isso faz com que mesmo que uma classe mais distante tenha muitas ocorrências, ela pode perder para uma que esteja mais perto e com menos ocorrência.

Esse mecanismo é interessante pois possibilita repartir o espaço em torno da instância que o K-NN irá classificar em pedaços.

Uma representação da divisão do plano em torno de um ponto.

É uma maneira interessante de pensar, mas perde precisões em grandes dimensões devido a perda de peso dos elementos do vetor, o que faz com que variáveis não tão importantes tenham a mesma influência que variáveis mais importante. O aumento da dimensão também faz com que a definição de longe e perto perca sentido devido a variação nos valores de cada elemento.

Isso acontece porque o K-NN (diferente de outros algoritmos), dá o mesmo peso para todos os elementos de um vetor. Por isso é interessante fazer uma análise de correlação nas variáveis que serão usadas para treiná-lo, e assim pode ser aplicado apenas nas mais relevantes.

Regressão.

Com algumas pequenas modificações, é possível aplicar o K-NN para problemas de regressões.

Assim como antes, podemos utilizar a distância Euclidiana para calcular a distância entre as instâncias, porém a diferença reside na forma em que será calculado o valor para instáncia, pois aqui, iremos associar um valor contínuo.

Ao invés de usarmos aquela classe que aparece com mais frequência no vetor dos vizinhos mais próximos, pegaremos uma média dos valores das classes dessas instâncias.

Agora suponha o conjunto de vetores pertencendo ao conjunto dos vizinhos mais próximos:

Como sabemos, cada vetor desse conjunto está associado à um valor real, pois o K-NN usa o próprio conjunto de treino como parte do algoritmo; logo, usaremos o vetor que representa esses valores. Então podemos associar a cada vetor do conjunto  à um valor real que representa seu valor.

Logo teremos o seguinte vetor que denomine :

A primeira estratégia que pode ser usada para se achar o valor da instância pode ser a média desses vizinhos mais próximos.

Então, o valor de saída nada mais seria do que a média dos vizinhos mais próximos daquela instância.

Apesar de interessante, na prática tendemos a ter variáveis fortemente enviesadas, aquelas que não seguem uma distribuição normal. Nesses casos, além de se fazer uma análise estatística da distribuição de nossa variável de interesse, é importante pensar em um método que nos ajude a desviar desse problema.

Para resolver isso, podemos utilizar uma média ponderada pelo peso das distâncias, como vimos anteriormente:

Então nesse caso, a função que associa um valor a instância que será classificada seria dada pela seguinte expressão:

Onde é o peso de cada valor real associado ao vetor dos vizinhos mais próximos.

E pode ser calculado como vimos anteriormente pela seguinte equação:

Onde é o vetor que queremos estimar o valor.

Mais uma vez separamos o espaço em partes, assim as instâncias em diferentes lugares do espaço terão diferentes pesos na formação do valor da predição.

Conclusão:

O mais importante na hora de se estudar o K-NN não é ó modelo em si, mas a estratégia usada para se estimar um valor, e as potenciais aplicações que vão muito além de mera classificação e regressão.

Quando fazemos isso, fica claro que o Bias do K-NN é associar valores semelhantes a instâncias semelhantes. Porém ele considera semelhantes instâncias que tenham o mesmo valor para seus atributos. Ele também trata cada instância de forma isolada, ao contrário de modelos como Decisions tree, ou as redes neurais que criam um modelo único para classificar ou estimar um valor para todas as instâncias.

Ele também associa o mesmo peso a todos os  atributos de uma instância, por isso é importante preparar e normalizar o conjunto de treino antes de aplicá-lo, e até mesmo selecionar os atributos necessários para usá-lo.

Outro ponto importante é que o K-NN se torna mais útil quando usado em conjunto com outros algoritmos, assim, um pode corrigir a fraqueza do outro aumentando a precisão.

O K-NN é um dos vários métodos que o cientista de dados, e engenheiro de Machine Learning utilizam no dia a dia para resolver alguns problemas práticos.

Mas, para entrar na carreira de dados é necessário um conjunto de habilidades, que vão desde da matemática pura e computação cientifica, à interação com o usuário final e regras de negócio.

Esse foi o post de hoje, qualquer sugestão ou crítica é sempre bem vinda. Bons estudos!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A ideia de Decision Trees para regressões

O modelo Decision Tree é muito famoso para utilização em classificação. Porem o que pouca gente sabe é que esse modelo também apresenta bons resultados em problemas de regreção.

Caso tenha pouco entendimento sobre esse modelo aconselho a dar uma lida nos posts abaixo.

Uma introdução a Decision tree

Entropia, Ganho de informação e Decision trees

Decision tree em python

Caso queira se aprofundar nos fundamentos matemático da área vale a pena dar uma confirida no curso abaixo:

Matemática para Data Science

Porem antes vamos definir o que é uma regressão no nosso contesto. Existem várias explicações e definições para o assunto, de uma olhada no wikipedia caso queira se aprofundar.

Mas para nosso contesto definiremos regressão como o ato de classificar um valor continuo com base em uma instância ou vetor.

Para quem já entende de Álgebra linear seria como uma transformada de  para .  Espero que tenha ficado minimamente claro a tarefa de hoje, caso não, continue lendo o post que as coisas darão uma clareada.

Exemplo de regressão linear simples

Em outras palavras: No contexto de Machine Learning Regressão é o nome dado ao ato de se associar um valor continuo a uma instância.

A principal diferença entre classificação e regressão é que enquanto na primeira as classes pertencem a um conjunto finito na segundo temos classe pertencendo a um conjunto infinito, geralmente dentro de um intervalo, mesmo assim com valores heterogêneos demais para serem contados.

Com isso definido vamos ao que interessa. Primeiramente precisamos de um Dataset para trabalharmos. Hoje eu trouxe um Dataset fictício que mostra variação no preço de uma ação semanalmente de acordo com 3 índices: variação no IPCA, variação no índice Ibovéspa e variação do Dólar.

Queremos saber a variação no preço de uma ação em função da variação desses índices.

O conjunto todo tem 25 instâncias separei 20 para treino e o resto deixarei para teste.

Uma vez tendo nossa tabela em mãos a missão agora é construir uma árvore que consiga nos dizer com maior precisão possível qual será a variação no preço da ação com base na variação desses três Índices.

Para quem já sabe o que é uma Decision tree a ideia é muito simples vamos substituir o score de referencia que geralmente é para classificação como Entropia ou Gini impurity por um que consiga lidar melhor com variáveis contínuas como Média e Variância por exemplo.

A maneira que escolhi para construir a árvore não a ideal, ainda mais para conjuntos de dados pequenos. Mas a missão aqui é te mostrar de maneira intuitiva como o modelo se desenvolve por isso usaremos esse método pela simplicidade.

Caso se interesse em aplicar o conceito te aconselho a não fazer exatamente dessa forma na prática pois existem vários detalhes que devem ser analisados, como instâncias, ruídos,  quantidade ideal de dados,  o tipo de distribuição probabilística do conjunto e mais um bocado de coisas.

Treinar um algoritmo para regressão com poucos dados é um pouco complicado pois pode não haver amostras o suficiente de uma determinada instância para o algoritmo captar padrões mais relevantes o que pode deixar as predições fracas.

Depois de algumas tentativas descobri que um jeito interessante de captar os melhores padrões é separar os dados pela média. Colocar de um lado os que são maiores e de outro os que são menores que a média e fazemos isso para cada coluna.

Depois disso medimos a variância da Label  de cada subconjunto e selecionamos aquele com menor variância para ser o novo ramo. Depois refazemos o processo para cada subconjunto.

Existem muitas formas modernas de se construir uma DT para regressões algumas mais simples e outras bem mais complexas optei por fazer dessa forma pela simplicidade com que o processo é feito.

Antes de começar vamos definir as técnicas que usaremos.

A boa e velha media é representada pela seguinte fórmula:

Onde é o número de elemento do vetor, no nosso caso serão as colunas, e é o valor do elemento.

A variância é representada pela seguinte fórmula.

A variância para quem não sabe funciona como uma média da diferença dos valores em relação a média.

Primeiro passo:

Calcula-se a média de todos os atributos\colunas menos a ultima pois essa é o alvo da predição.

media(Ipca) = 0.10

media(Ibovespa) = -0,12

média(Dolar) = 0.15

Depois disso separamos as instâncias. Vamos colocar as que são menores ou iguais a média de um lado e as que são maiores em outro. Fazemos isso para cada atributo.

E claro calculamos a variância label Ação para cada conjunto

Isso feito teremos o seguinte esquema.

Isso feito pegamos o atributo que melhor divide o Dataset em dois, repare que isso é uma forma de captar uma correlação entre o valor do atributo e o preço. A ideia é dividir em grupos cada vez mais semelhantes onde a variância na variação do preço da ação seja cada vez menor.

Escolhemos o Dolar pois um de seus subconjuntos tem a menor variância isso quer dizer que as instâncias são menos dispersas ali.

 Repare que agora temos o nosso primeiro discriminante

Com isso feito repetimos o processo para cada ramo.  Tiramos a média e separamos os maiores de um lado e os menores de outro,  fazemos isso para cada atributo e selecionamos aquele que melhor divide o conjunto.

Para fins didáticos usareis como folha o Node que tiver 3 ou menos amostras, pois se fazer o processo indefinidamente pode levar a árvore a overfitting. Apesar de não ser o melhor jeito a definição do número de elementos mínimos para ser uma folha é muito usado para evitar overfitting.

Se repetimos o processo teremos a seguinte estrutura:

Vamos repetir o processo mais uma vez agora para cada um dos 3 subconjuntos formados.

Repare que agora temos uma folha na árvore, isso aconteceu pois a quantidade de amostras naquele ramo chegou em 3,  então usei a média dos preços das ações que compunham essa amostra como output.

Vamos realizar mais uma iteração para ver como fica a estrutura.

Repare que ainda faltam 5 instâncias para usarmos para treino vamos repetir o processo. Depois de feito teremos a seguinte estrutura.

Você pode testar no conjunto de teste. Infelizmente ela não tem um desempenho tão bom pois usamos poucos dados para treino mesmo assim o resultado é interessante.

O Erro médio absoluto fica em torno de  0,312.

Confesso ser muito bom apesar do método usado e da quantidade de dados.
Então é isso esse foi o post de hoje.

Caso queira se aprofundar no assunto um excelente curso em português é:Launching into Machine Learning em Português Brasileiro

Como sempre qualquer dica, critica ou erro encontrado no post não exite em deixar nos comentários.

Ate a próxima e bons estudos.

Entropia, Ganho de informação e Decision trees

Ola pessoas, primeiramente já irei avisando que o post de hoje tem matemática sim, infelizmente em ML caso queiramos entender de fato os algoritmos é crucial termos a capacidade de lidar com alguns cálculos relativamente complexos. O que é chato para alguns mas eu adoro, mas não precisa se desesperar vamos usar um exemplo leve.

O exemplo de hoje foi baseado no livro Machine learning de Tom M. Mitchell claro que fiz algumas modificações para ficar mais leve e ajudar você leitor a entender melhor essas medidas e adaptá-las a seu modelo de aprendizado.

Muito bem para você que leu Introdução a decision tree percebeu que eu usei uma simples histograma para escolher os melhores atributos para os Nodes. Mas para classificarmos um conjunto de dados mais complexos essas medidas talvez não sejam as mais apropriadas.Eu usei os conceitos apresentados aqui hoje no post Decision tree em python.

Para esse exemplo vamos usar um conjunto de dados simples:

A tabela acima consiste em um conjunto de treino com 14 instâncias cada uma com 4 atributos, a primeira coluna é apenas para contar os dias e a última representa as classes de cada instância.

Vamos fazer algumas análises nesse conjunto de treino.

Entropia

A entropia é normalmente usada na teoria da informação para medir a pureza ou impureza de um determinado conjunto. A pergunta que ela responde é: O quanto diferente/iguais esses elementos são entre si? Claro que as aplicações desse conceito vai muito além da teoria da informação mas vamos manter as coisas humildes.

Vemos ao lado o clássico exemplo da entropia sendo aplicada a um conjunto de dados binários.

No caso, colocando no eixo das abscissas a proporção de exemplos positivos dos conjuntos.Na origem vemos que temos zero exemplos positivos o que implica em uma entropia igual a zero pois temos um conjunto todo negativo.

Quando a proporção de exemplos positivos chega a 0,5 temos o grau mais alto de entropia, pois em um conjunto binário esse é o ápice da mistura, depois ela vem diminuindo outra vez.

Pense sobre a figura acima um pouco e tente captar o conceito.

Abordaremos a fórmula de maneira bem prática o intuito é que você leitor consiga entender e reproduzi-la facilmente em código.

Primeiramente é a proporção de exemplos em relação a todo conjunto e é o número no qual temos que elevar 2 para chegarmos ao valor em questão temos também que é o número de classes que estamos usando.

Vamos calcular a entropia de todo o conjunto. Voltando na tabela vemos que temos 5 exemplos positivos e 9 negativos, é muito comum usar a notação [9+,5-], como a entropia é um somatório de todos os temos que:

Antes de fazermos os cálculos mostrarei uma propriedade dos logaritmos muito útil para você que ira utilizar calculadora para realizar os cálculos. Pois geralmente as bases usadas são 10:

Vamos a um exemplo óbvio.

Ou seja 2 elevado a 3 é igual a 4.

Uma importante observação é que quando formos calcular   de 0 iremos assumir que é 0 ,por motivos que espero esclarecer no futuro, e claro para valores igual 1 teremos também um valor igual a 0. Todo número elevado a 0 é igual a 1.

Voltando ao exemplo anterior temos:

Então essa é a entropia total do conjunto também representa a entropia de cada coluna/atributo. Esse índice será usado como parâmetro para outros índices um deles é o ganho de informação.

 

 

 

O ganho de informação

Uma vez medida a entropia do conjunto podemos aplicar o ganho de informação para selecionar o melhor atributo para ser o primeiro Node de uma árvore por exemplo.

Eu sei que parece chato a primeira vista mas não é nem um bicho de sete cabeças. Vamos interpretar com bastante calma essa fórmula.

Vamos analisar a seguinte notação primeiro o S representa o conjunto todo e A representa o atributo em questão.

Lembre-se que um atributo é representado por uma coluna logo podemos fazer uma análise de todos os atributos e selecionar aquele que tem o maior ganho de informação.

Quando vemos estamos nos referindo a um somatório aplicado a valores de um conjunto, será feito uma iteração para cada valor desse conjunto, no caso os valores do atributo. é a proporção da frequência de v em relação ao conjunto todo e depois multiplicamos isso pela entropia do subconjunto que contem esses valores para esse atributo.

O ganho de informação nesse contexto nos permite criar um índice para medir qual o melhor atributo para ser o primeiro Node da árvore.

Vamos aos cálculos:

Consideramos que a entropia do conjunto todo vale 0.939 com isso podemos calcular o ganho de informação do primeiro atributo expectativa. Vamos antes disso criar uma tabela de frequência com os valores da primeira coluna.

Temos quatro colunas com a frequência relativa de cada valor juntamente com a ocorrência de valores positivos e negativos em cada um.

Com isso podemos calcular o ganho de informação da primeira coluna e saber se ela é um bom atributo para ser a raiz da árvore.

Então teremos:

Como vimos para calcular a entropia do conjunto usamos   fazendo isso para cada subconjunto de Expectativa teremos:

Logo:

Fazendo o mesmo processo nos outros conjuntos:

A conclusão que tiramos é que o melhor atributo seria Expectativa para ser a raiz da árvore.

Vamos apenas para exemplificar a situação começando a construir a árvore de duas maneiras diferentes.

A primeira fazendo o Atributo como Node e os Ramos como seus valores ficaria dessa forma:

Usamos o primeiro Atributo para ser a raiz da árvore e cada ramo representa um conjunto de instâncias que por sua vez devem ser avaliadas para formar novos ramos.

Com exceção do Ramo nublado pois segundo o conjunto de treino quando Expectativa = nublado é certo que é um exemplo positivo.

Poderíamos também fazer uma árvore binária, neste caso procuraremos dentro do Atributo com maior ganho de informação o valor com a menor entropia.

Para nossa sorte fica claro que quando Expectativa=Nublado a classe da instância é certamente positiva logo podemos usar este valor para ser o primeiro Node da árvore.

Repare que quando a resposta é não ainda tem várias instâncias a serem classificadas, caso se interesse em continuar fazendo o processo é o mesmo.  Basta supor que esse Node é uma nova árvore e continuar o processo de medir o ganho de informação e selecionar o melhor atributo, no caso do primeiro exemplo, ou selecionar o melhor atributo e valor no segundo caso.

Muito bem queridos leitores. Para aqueles que tiveram a paciência de chegar até aqui, meu muito obrigado. Primeiramente por ler esse post, isso é importante para mim,  e  que tenha sido útil para você continuar desenvolvendo seus skills nesta área fascinante.

Agora se você quer aprender mais sobre teoria da informação e suas aplicações não deixe de conferir o curso Information Theory que você acha no site Coursera.

E qualquer dúvida, feedback, crítica ou erro de cálculo não se acanhe deixe nos comentários.

Até o próximo post.

 

 

 

 

 

Formalizando um problema de aprendizado de Maquina

Ola queridos leitores, no poste de hoje irei trabalhar um pouco com a definição de um problema de Machine learning, usarei alguns exemplos simples para facilitar a vida daqueles que estão interessados nessa área fascinante.

Quando estamos lidando com um problema de Machine Learning a algumas coisas  coisas que temos que levar em conta.

-Temos que testar a performance de nosso algoritmo o aplicando em um conjunto de teste, é importante salientar aqui que esse não pode ser o mesmo usado para treinar o algoritmo.

-A maneira que medimos a performance ira depender do tipo de problema que estamos tentando resolver, lembre-se que cada tipo de tarefa requer um cuidado próprio.

-Deve haver um forte relação entre o conjunto de dados que nosso algoritmo estará usando para treinar e o conjunto de dados em que iremos testa-lo é comum dizer que ambos devem ter a mesma distribuição.

Lembre-se não adianta estudar matemática e fazer uma prova de historia.

Para medirmos o desempenho de nosso algoritmo durante o treino é comum utilizar uma Loss function esta função ira nos ajudar a medir o erro de predição no conjunto de treino durante o treinamento do algoritmo.

Agora suponha que seja nosso input, para entendermos melhor um input nesse caso seria um objeto com suas características,geralmente um vetor com variáveis reais ou discretas, por exemplo se  iremos treinar um algoritmo para reconhecer fotografias o input seria uma fotografia e o output seria a identificação dessa fotografia, então para efeito de cálculo vamos chamar o output de  quando estamos testando o algoritmo o que teremos é um conjunto de pares ordenados contendo os inputs e outputs no caso seria : .

Para medirmos o erro basta que apliquemos a função de perda em cada par ordenado onde é o output esperado, mas você deve esta se perguntando que função é essa.

Isso vai depender do tipo de problema, caso tenhamos um problema de regressão onde o output é um número real podemos usar o Squared loss que é dado por ou o Absolute loss que é dado por .

Já para problemas binários do tipo verdadeiro ou falso, sim ou não dentre outros podemos utilizar a zero/one loss function.

O no caso acima se refere a diferença entre e geralmente associamos números aos outputs mas ate onde sei nada impede de usar outros métodos.

Essa função também pode ser usada para medi o erro em problemas de múltiplas classes com os devidos ajustes, note também que as funções para medir o erro são modeladas de acordo com a necessidade de medição o tipo de predição.

Agora que nos definimos as funções para medir o erro é necessário saber de onde vem o nosso Conjunto de treino e o Conjunto de teste.

Antes vamos deixar claro que não irei me aprofundar no assunto aqui pois existe varias maneiras de gerar um conjunto de treino, porem eu aconselho usar uma Distribuição aleatória uniforme dos dados no inicio.

Uma distribuição aleatória uniforme consiste em pegar do conjunto de teste amostras aleatórias porem de maneira uniforme para treinar nosso algoritmo.

Esse método é interessante pois diminui a probabilidade de pegar um objeto sem sentido, por exemplo: se eu estou usando um banco de dados sobre pássaros para treinar um algoritmo, e nesse conjunto de dados existem três características, sejam elas: cores das penas, tamanho do bico e tamanho das pernas, e os outputs sejam canário,sabiá e coruja.

Na hora de escolher os dados é importante se atentar a proporção dos dados que estamos pegando, pois dependendo da estrutura pode surgi vários problemas, mas como já disse não irei discorrer sobre isso agora.

Dai vale a pena pegar uma amostra aleatória do conjunto de teste para treinar  o algoritmo, no mais devemos pegar de maneira uniforme para aumentar a eficácia pois se eu pegar de maneira totalmente aleatória poderia estar pegando muito de um tipo de dado e pouco de outro tipo ou quem sabe não pegar um tipo de dado e assim não treinar o algoritmo de maneira correta.

Então podemos formalizar o problema da seguinte maneira, dado um conjunto de dados com objetos do tipo onde são as características e são os outputs esperados podemos ter um conjunto de treino onde  que podemos ler como “para todo input e output pertencendo ao conjunto de treino é proporcional a todo input e output pertencendo ao conjunto de dados.

Em resumo, quando queremos treinar um algoritmo podemos pegar uma amostra aleatória do conjunto de dados de modo que os exemplos nele contido sejam proporcionais aos exemplos no conjunto de dados.

Feito isso, nosso problema pode ser definido em duas partes.

-A medição do erro por meio da função , o método usado ira depender da tarefa a ser aprendida .

-E o nosso conjunto de treino que é uma amostra aleatória porem estratificada do conjunto de dados.

Nossa missão agora é aplicar o algoritmo no conjunto de dados de modo que diminuamos o erro ao máximo, porem para fazermos isso precisamos calcular o erro total que pode ser definido da seguinte forma.

onde   é nosso erro esperado, é quantidade de exemplos no conjunto, é o algoritmo aplicado ao input o que gera um output assim se ele estiver errado acrescentamos ao somatório, caso contrario não, e o  sendo o valor esperado, repare que se for um problema binário será somado apenas 0 ou 1 se for um problema de regressão será somado a diferença do output ao valor real.

Mas não precisa se apegar muito a equação acima pois em futuros post  ainda irei emprega-la em contesto melhor. Mesmo assim ela é bem simples de entender, a questão aqui é quando formos treinar um algoritmo nossa missão é reduzir ao máximo a margem de erro.

Claro que podemos reduzi-lo a zero bastando para isso adapta-lo ao  ao conjunto de treino porem a missão é capacita-lo para ir além do conjunto de treino ou seja generalizar ao máximo. Pois assim teremos um algoritmo capaz de reconhecer com eficácia as características de um objeto e ira reconhece-lo em varias situações.

Lembrando aqui que reduzir o erro a zero enquanto estiver treinando o algoritmo não é uma boa ideia isso ficara claro em futuros posts.

Agora podemos juntar tudo e criar uma definição formal para qualquer problema de aprendizado:

Dado um algoritmo de aprendizado nosso intuito é aplica-lo a um conjunto de teste de modo que que tenhamos uma margem de erro o mais próximo possível de zero.

Uma vez realizada essa tarefa teremos em nossa mãos um algoritmo com um bom desempenho e pronto para ser aplicado em situações concretas e em conjuntos de dados ainda não vistos.

Repare também que aqui começa a ficar claro a ideia de Aprendizado supervisionado pois estamos aprendendo a mostrar para o algoritmo o que é  certo e o que é errado. É supervisionado pois nos temos acesso ao que é certo e ao que é errado.

Antes de encerrar o post quero indicar um livro que achei muito legal e me ajudou muito a entender alguns conceitos.

É o livro é Machine Learning: Introdução à classificação. Apesar de tratar apenas de problemas de classificação é um excelente porta de entrada para se lidar com problemas de machine learning

Mas se você é do tipo que se identifica mais com cursos. Sem duvida irá gostar do curso Mathematics for Machine Learning

Ele trata justamente das definições de problemas de aprendizado de maquina de maneira formal e do ferramental matemático para se fazer isso.

 

Caso  goste deste poste provavelmente ira gostar destes dois posts:

O problema do aprendizado. e Alguns problemas de aprendizado.

Se você leu ate aqui muito obrigado e qualquer critica, opinião ou duvida desde que sejam construtivas é extremamente bem vindas. 🙂

problemas básicos em aprendizado de maquina

Ola meus queridos 7 leitores como prometido trago mais um post sobre os problemas envolvidas em um modelo de machine learning, hoje vamos analisar alguns problemas básicos e aprender mesmo que de maneira superficial diferencia-los, isso pode ser útil na hora de modelar seu algoritmo.

Existe inúmeros problemas de aprendizados por indução, e é importante se atentar a maneira que cada um lida com erro pois isso afeta diretamente na eficácia do algoritmos. Vamos analisar alguns problemas de aprendizado bem básicos e discorrer um pouco sobre suas aplicações e maneira que cada um lida com o erro.

Regressão: Em problemas de regressão estamos interessado em achar um número real com base é informações passadas, é interessante se atentar que os tipos de dados envolvidos são geralmente contínuos.

É muito comum lidar com esse tipo de problema em mercados financeiros onde com base nos preços passados das ações tentamos achar um aproximação das futuras cotações. Uma maneira de medir o erro nesse tipo de problema é pegarmos o valor alvo, e subtrair dele o valor gerado pelo algoritmo, quanto menor o valor absoluto maior a eficácia do algoritmo.

 

Classificação binária: Nos problemas de classificação binária o objetivo é separar o conjunto de dados em dois, por exemplo em SIM ou NÃO, 0 ou 1, X ou Y e assim por diante.

Geralmente esses problemas são mais elementares, apesar de estarem na mesma classe dos problemas de classificação é importante identifica-los pois assim podemos aplicar algoritmos mais específicos para essas situações.

Nos problemas de classificação binária os dados são geralmente discretos, uma aplicação interessante seria em classificar um visitante de uma pagina como sendo homem ou mulher a partir dos links em que ele(a) clicou.

Medir o erro nesse tipo de problema é diferente das regressões pois só temos duas opções ou se esta certo ou errado, geralmente associamos 1 a certo e 0 a errado.

 

Classificação de múltiplas classes: Nesse tipo de problema o interesse é classificar varias classes de acordo com as características que elas tem em comum, os dados podem ser tanto contínuos como discretos.

Esse tipo de problema é muito comum desde de sistemas de indicações, reconhecimento de objetos, na medicina, biologia ate na astronomia para classificar corpos celestes.

Um exemplo de algoritmo de classificação pode ser visto nesse artigo: K-nearest neighbors seu primeiro algoritmo de machine learning.

Medir o erro nesse tipo de problema é bem parecido com a classificação binária ou estar certo ou errado, porem a diferença é que podemos usar mais critérios como a proximidade entre duas classes por exemplo.

 

Ranking: Nesse tipo de problema o interesse é rankear os objetos dados suas características especificas. Geralmente acontecem quando queremos rankear os produtos que tem potencial de vender mais com base nas semelhança com outros produtos, quais doenças um paciente tem mais probabilidade de desenvolver com base em seu histórico médico dentre outros.

Medir o erro em um problema de rank requer o uso de técnicas mais sofisticadas e acho melhor falar disso em outro post mais especifico.

Bem se você chegou ate aqui saiba que significa muito para mim e qualquer critica, sugestão ou duvida desde que sejam construtivas são extremamente bem vindas muito obrigado e ate o próximo post.

 

 

 

Aplicações de soma e multiplicação de matrizes

Apesar de simples, a multiplicação é muito utilizada no dia a dia de qualquer profissional que lide de alguma forma com análise de dados. Podemos utilizar essa estrutura para modelar vários problemas práticos.

Soma de matrizes.

A soma de matrizes não é algo difícil, alias é muito intuitivo, então vamos logo a exemplo:

Uma pessoa possui 3 paginas no Facebook e quer criar algumas métricas para medir o desempenho delas. Como sabemos quando publicamos algo no Facebook existem 3 categorias básicas de interação com o mesmo que são: comentários,curtidas e compartilhamentos, muito bem, com esses dados é possível criar uma tabela para cada mês de vida das paginas.

Observação: os valores que aparecem na tabela são aleatórios não precise ficar preocupado com  de onde eu tirei eles.

desempenho da pagina no mês 1.

Como vemos fica fácil tirar algumas informações interessantes quando colocamos nesse formato, como qual é a pagina que tem mais curtidas, ou a que tem mais compartilhamentos e por ai vai.

Agora vamos criar uma tabela para o segundo mês para podermos tirar mais algumas informações interessantes e aplicar a soma de matrizes.

Desempenho da pagina mês 2

Agora temos duas tabelas uma para o mês 1 e outra para o mês 2, agora vamos coloca-las em notação matemática.

Vamos chama-las de e :

    e    

Antes gostaria de lembrar sobre como localizar um elemento de uma matriz vamos por exemplo ver a matriz o representa as linhas e o representa as colunas.

então se eu me referir ao elemento eu estou falando do número 85 na matriz .

A soma delas será dada por , só lembrando que para somarmos matrizes somamos cada elemento da matriz com o elemento correspondente na outra matriz.
então neste caso:

Bem simples não?. Chamaremos essa nova matriz de , da mesma forma se quisermos  saber a diferença entre essas matrizes basta somarmos a matriz com o oposto da matriz   que seria basicamente  trocar todos os sinais dos elementos dessa matriz por negativo.

Agora vamos aproveitar para discorrer um pouco sobre a notação de  somatório muito usada em operações com matrizes e séries.

Vamos supor que temos a seguinte soma:

Fiz dessa forma pois quero dizer que estou somando um número indefinido de matrizes, isso acontece muito em banco de dados, planilhas e qualquer outra base de dados em que exista uma atualização constante então é melhor optar pelo sigma.

Com isso estou dizendo que somarei as matrizes do primeiro mês ate a matriz do mês. Entenda por mês o ultimo mês ate onde quero somar repare que no somatório o na parte de baixo é o limite inferior é onde começa a soma e o é o limite superior é onde termina a nossa soma.

por exemplo:

Bem sobre soma de  matrizes pararei por aqui poderíamos analisar mais casos porém isso envolve outras operações e eu queria tratar apenas da soma de matrizes em si e desmistificar um pouco a notação de somatório.

Multiplicação de matrizes.

Agora vamos ver uma aplicação da multiplicação de matrizes.

Supomos que alguém resolve aplicar na bolsa de valores e compra algumas ações no caso as ações A, B, C e D. Ele compra as seguintes quantidades de cada:  19 da A, 12 da B, 73 da C e 46 da D. E como sabemos cada ação tem seu preço unitário para este exemplo podemos dizer que A custa R$ 8,00, B custa R$ 7,00, C custa R$ 6,00 e D custe R$ 9,00 pede-se que calcule o total gasto para comprar essas ações.

Para ajudar com o raciocínio vamos organizar esses dados em tabelas.

Como você pode ver eu organizei as tabelas de um jeito não muito ortodoxo, você já vai entender porque fiz dessa forma.

Mas antes de discutirmos isso vamos dar uma olhada como que é feita a multiplicação de matrizes.

supomos as seguintes matrizes:

  e

Existe algumas definições formais para multiplicações de matrizes mas eu irei utilizar uma maneira mais pratica.

A multiplicação das matrizes acima vai ficar dessa forma.

A primeira regra que temos que lembrar é que para multiplicar duas matrizes o número de linhas da primeira deve ser igual ao número de colunas da segunda.

e a matriz resultante terá o mesmo número de linhas da primeira e mesmo número de colunas que a segunda vamos chama-la de , com base nessas informação sabemos que a matriz será quadrada 2×2 vamos obter o elemento da primeira linha e primeira coluna dessa matriz ou elemento :

pegamos a primeira linha da matriz  e multiplicamos pela primeira coluna da matriz :

=

pronto temos o o elemento gora iremos repetir o procedimento ate achar todos os elementos.

=
=  
=

Agora que já temos todos os elementos da matriz vamos organiza-la.

pronto fizemos a multiplicação de matrizes, agora vamos voltar a nosso exemplo inicial.

Vamos primeiro colocar essas tabela como matrizes vamos fazer a matriz de preços e a matriz de quantidades:

   e   

Feito isso basta realizar o mesmo procedimento citado acima as linhas da primeira matriz vezes as colunas da segunda e obtemos como resultado 1088 no caso teremos uma matriz de uma linha e uma coluna.

Mas agora vamos deixar as coisas mais interessantes. como sabemos os preços das ações variam com o passar do tempo devido as intempéries do mercado, então iremos acrescentar mais uma linha a nossa matriz de preços, a linha preço de venda, para sabermos como uma variação em um dos elementos da linha afeta o lucro do acionista.

Agora olhe que a primeira linha da matriz é o preço de compra e a segunda é o preço de venda assim temos :

   e   

realizando a multiplicação teremos a seguinte matriz que chamarei de :

Na primeira linha temos o custo das ações e na segunda o valor que ele ganhou vendendo elas ou seja ouve um lucro, antes de finalizarmos vamos acrescentar mais uma coluna na tabela de quantidades.

Repare com calma, agora houve uma variação  na quantidade de ações por exemplo a ação A possuía uma quantidade de 19 depois passo para 73, o mesmo ocorre com as outras, vamos analisar como isso afeta o lucro e o valor de compra nesse cenário.

Primeiro vamos redefinir as matrizes:

  e 

Depois de realizarmos a multiplicação de matrizes usando o método já explicado acima vamos obter a seguinte matriz:

Observe a primeira coluna da matriz temos o preço de compra e venda com a primeira quantidade e na segunda coluna temos o preço de compra e venda com a segunda quantidade nesse caso ele teria um prejuízo.

Tente assimilar a operação de multiplicação e depois observar com bastante calma a matriz resultante e a tabela.

Muito bem caro leitor se você leu ate aqui muito obrigado pela atenção, é claro que esse exemplo é só ilustrativo, poderíamos acrescentar uma quantidade muito maior de linhas e colunas nessas matrizes alias é isso que ocorre na vida real, principalmente quando querem simular vários cenários para um determinado acontecimento.

E não esqueça que calcular usando matrizes é uma tarefa trabalhosa por isso na pratica usamos softwares ou linguagens de programação como Python e R por exemplo.

E por fim se você que leu esse post não gostou não se acanhe fale o porque que eu trato de fazer melhor na próxima, pra você que leu e gostou mas achou que pode ficar melhor só deixar uma dica nos comentários que estará me ajudando muito.

Antes de terminar de vez. Fique sabendo que esse poste é apenas uma pontinha do que a Algebra Linear tem a oferecer em ferramental. E eu acredito fortemente que o melhor jeito de aprender matemática é acompanhado a teoria e fazendo exercícios. Para esse fim eu recomendo fortemente a apostila da Top Apostilas  Apostila Álgebra Linear. Eles conseguiram juntar uma variedade interessante de exercícios que vai te permitir  entender muito bem vários tópicos da área.

Infográfico sobre cojuntos e funções.

Ola pessoas, hoje  resolvi fazer algo que espero que seja útil para que esta se preparando para vestibulares, concursos e outras provas em geral.

As pessoas as vezes me pergunta o que estudar primeiro e quais os pré requisitos em cada matéria. A partir disso decidi criar um série de infográficos para mostrar todas as matérias relacionadas a um tema e seus pré requisitos.

Esse primeiro infográfico é sobre funções e conjuntos e foi baseado no livro Matemática elementar volume 1 de Gelson Iezzi e Carlos Muramaki livro maravilhoso para quem quer  ter uma base sólida sobre o assunto.

Observando que as vezes o estudante quer aprender apenas alguns tópicos coloquei os pré requisitos necessários para cada tópico.

Muito bem, esse foi meu primeiro infográfico sobre o assunto o próximo com certeza será um pouco melhor.

E qualquer sugestão e critica construtiva é extremamente bem vindas pois isso me ajudara a melhorar ainda mais meu próximo post.

Usando matrizes para interpretar algumas relações.

Ola para você que esta lendo esse post, hoje resolvi escrever sobre uma coisa um pouco mais acadêmica, Matrizes, mas antes de começarmos os cálculos e tal quero te dizer que não precisa ficar com  medo. Não iremos utilizar muitos cálculos, é mais uma coisa conceitual.Também não é uma aula sobre matrizes. É mais uma demonstração de algumas de suas aplicações.

O motivo para escrever sobre este tema é que venho reparando o aumento constante de pessoas interessadas em Data science, Machine learning, Data analysis e varias outras áreas interessantes que lidam com dados.

E entender o conceito de matriz é muito importante para lidar com dados e relações entre eles. Para você que se interessou pelo post e quer continuar lendo ira precisar de apenas alguns pré requisitos: saber somar duas matrizes, e multiplicação de matrizes mas não se preocupe se você não lembra mais.

observação importante: posso usar alguma notação estranha mais não se espante se você não tem uma boa base, eu explico como funciona o importante é você conseguir imaginar o conceito.

Primeiro vamos aos dados.

Meu intuito nesse exemplo é mostrar como medir relações entre pessoas ou objetos, vou usar como exemplo o Twitter .

Suponha 5 pessoas que utilizam o twitter, a relação mais básica que podemos analisar é quem segue quem, então iremos explorar isso. Como sabemos no Twitter eu posso seguir ou ser seguido por uma pessoa, os mais famosos tem mais seguidores do que os menos famosos.

Tudo bem óbvio, mas agora  vamos  dar nomes aos nossos elementos.

Supomos agora que eu tenha um conjunto de 5 perfis do Twitter  ou seja os perfis perfil 1,perfil 2,perfil 3,perfil 4,perfil 5 podemos representar por meio de notação matemática:

 

Agora vamos supor que estas pessoas seguem umas as outras, como sabemos no Twitter o fato de o perfil 1 seguir o perfil 2 não que dizer que o perfil 2 vá seguir o perfil 1 de volta ou seja queremos saber como o conjunto perfil se relaciona com ele mesmo.

Há varias formas de pensarmos isso mais eu prefiro usar um diagrama para expressar as relações entre estes Twitters.

 

No diagrama observe as setinhas. Repare que o perfil 1 por exemplo segue o perfil 3 e é seguido pelo perfil 4, o perfil 2 segue o perfil 3,4 e 5 e não é seguido por ninguém.

Essa forma pode ser interessante quando se tem poucos dados, porem quando se trata de uma quantidade muito grande é mais interessante usar uma matriz.

Vamos representar o mesmo exemplo só que por meio de uma tabela:

observação: vou utilizar os números 1 e 0 para denotar se um perfil segue ou não o outro.

1 para segue e 0 para não segue.

observe a tabela que vai ficar mais claro.

Repare que quando um perfil segue o outro eu usei o numero 1, por exemplo: Olhe a linha do perfil 1 ele não segue ele mesmo(o que nunca vai acontecer.), ele não segue o perfil 2, ele segue apenas perfil 3 e assim por diante.

Se você reparar nessa tabela vera que as linha dizem se um perfil segue ou não o outro, enquanto que as colunas dizem se um perfil é ou não seguido por outro.

Repare que o perfil 3 é o que tem mais seguidores, o perfil 1 é o que seguem menos pessoas. da para tirar muita informação legal tudo depende do que você quer saber e o tamanho de sua base de dados.

Mas ainda da para responder mais perguntas.

Se querermos descobrir algo mais especifico, como quantas perfis o perfil 2 segue que por sua vez sigam o perfil 3, ou o contrario quantos pessoas seguem o perfil 3 são seguidas pelo perfil 2 ?

A partir de agora vamos introduzir a notação de matriz, vamos representar a tabela a cima por meio de uma matriz pois fica mais fácil realizar os cálculos .

vamos chama-la de Mr(matriz de relações.).

Muito bem agora iremos elevar essa matriz ao quadrado ou seja multiplicar ela por ela mesma.

Mas antes uma parada rápida.

Agora para quem não lembra como ocorre a multiplicação de matrizes não tem problema mas seria interessante aprender no futuro pois além de ser fácil é muito útil.

para os mais experientes em matemática segue a definição  para  multiplicação de matrizes.

dadas as matrizes: e o produto dessas matrizes é dado por onde:

 

Basta utilizar esta formula para cada elemento  da nova matriz, mas aconselho a fazer isso por meio de uma ferramenta. Se você tem conhecimentos em programação facilita muito o trabalho, Python é muito bom basta utilizar o Numpy.

Agora se você não saca de matemática nem de programação não tem problema foque nos conceitos mais simples como a relação entre os perfis e tente entender a tabela.

pois o que interessa é mais o  significado da matriz ao quadrado do que saber as técnicas para fazer isso.

Mas é claro que se você gostar pode se aprofundar em Álgebra linear.

Voltando com o problema.

como vimos estabelecemos a matriz  e para eleva-la ao quadrado fica:

=

 

ou seja

 

Agora vamos colocar essa matriz em uma tabela e compara-la com o anagrama novamente para podermos interpretar o que isso significa.

 

 

Olhando a linha do perfil 1.  quando cruzamos o perfil 1 com o perfil 2 o número é 0, isso que dizer que o perfil 1 não segue um perfil que também segue o perfil 2.

Quando cruzamos o perfil 1 com o perfil 4 vemos um número 1, isso que dizer que ele segue uma pessoa que segue o perfil 4, no caso o perfil 3, basta olhar a setinha que sai do perfil 1, ela vai para o perfil 3 e esse por sua vez liga ao perfil 4.

No caso se cruzarmos o perfil 2 com perfil 3 vemos o número 2 o que significa que o perfil 2 segue duas pessoas que seguem o perfil 3, no caso o perfil 4 e o perfil 5.

A partir disso podemos achar algumas aplicações interessantes tudo depende do tipo de informação que estamos procurando, é claro que na vida real as coisas são bem mais complicadas isso só foi um exemplo simplista para mostrar algumas funcionalidades das matrizes e o que acontece quando elevamos uma matriz ao quadrado.

se você gostou e saca de matemática pode tentar resolver o desafio que é interpretar o que significa:

+

E se você leu ate o final muito obrigado e ate a próxima :).